▷ Determinantes | Cuáles hay y cómo resolverlos

Lo primero que hay que tener en claro es que un determinante siempre se tiene que trabajar de $n\times n$ , a lo que nos referimos es que tiene que ser una matriz cuadrada. Nota: más adelante veremos los determinantes de los sistemas de ecuaciones lineales.

El símbolo del determinante para las matrices de orden $n$ se representa como $\Delta_{n}$ , un determinante de $n \ filas$ y $n \ columnas$ , ahora lo vemos a continuación, tranquilo. Hay autores que utilizan una letra para representar a las columnas y un número como subíndice para representar a las filas:

\Delta_{n} = \left| \begin{array}{c c c c} a_{1} & b_{1} & \dots & z_{1} \\ a_{2} & b_{2} & \dots & z_{2} \\ \dots & \dots & \dots & \dots \\ a_{n} & b_{n} & \dots & z_{n} \end{array} \right|

Y hay autores que utilizan la misma letra como base y sus subíndices significan las filas y las columnas respectivamente, eso quiere decir que $a_{2 1}$ hace referencia al valor que se encuentra en la fila 2, columna 1, veamos el ejemplo:

\Delta_{n} = \left| \begin{array}{c c c c} a_{1 1} & a_{1 2} & \dots & a_{1 n} \\ a_{2 1} & a_{2 2} & \dots & a_{2 n} \\ \dots & \dots & \dots & \dots \\ a_{n 1} & a_{n 2} & \dots & a_{n n} \end{array} \right|

Con eso ya estamos listos para pasar a los ejemplos, la notación que utilizaremos es la del segundo ejemplo.

Determinantes de segundo orden

Cuando hablamos de determinantes de segundo orden, hablamos que calcularemos determinantes de matrices cuadradas de $2\times 2$ . Calculemos el determinante de la matriz $l$ :

l = \left[ \begin{array}{c c} 3 & 5 \\ 2 & 6 \\ \end{array} \right]

Para el cálculo de los determinantes de las matrices de $2\times 2$ , se tiene que multiplicar los números de la diagonal azul menos la multiplicación de los números de la diagonal roja:

$\Delta_{A} = a_{11}\cdot a_{22} - [a_{21} \cdot a_{12}]$

Bien, ahora procedamos a calcular el determinante de la matriz $l$ :

\Delta_{l} = \left| \begin{array}{c c} 3 & 5 \\ 2 & 6 \\ \end{array} \right| = 3\cdot 6 - [2\cdot 5] = 8

Así que observamos que el determinante de la matriz $l$ es igual a $8$ .

Eso es todo lo que se necesita para calcular determinantes de matrices de $2 \times 2$ .

Determinantes de tercer orden

Para el cálculo de las determinantes de tercer orden utilizaremos algo peculiar que sólo es para que se haga más cómodo a la vista, que es añadir dos columnas más, pero cuando tomes algo de práctica, la determinante la realizarás sin hacer ésto de añadir las dos columnas más. Bien, veamos nuestra siguiente matriz:

B = \left[ \begin{array}{c c c} 5 & -1 & 3 \\ 3 & 5 & -4 \\ 7 & -2 & 3 \end{array} \right]

Para el cálculo del determinante de la matriz $B$ , vamos a agregar una vez más las dos primeras columnas:

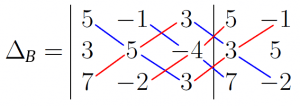
\Delta_{B} =\left| \begin{array}{c c c | c c} 5 & -1 & 3 & 5 & -1 \\ 3 & 5 & -4 & 3 & 5 \\ 7 & -2 & 3 & 7 & -2 \end{array}\right.

Ahora, para calcular el determinante de la matriz $B$ , vamos a sumar la multiplicación de cada diagonal azul y luego vamos a restar la sumatoria de cada multiplicación de cada diagonal roja, visualmente es así:

$\Delta_{B} = 5\cdot 5 \cdot 3 + (-1)\cdot (-4) \cdot 7 + 3\cdot 3 \cdot(-2) -$

$\left[ 7 \cdot 5 \cdot 3 + (-2) \cdot (-4) \cdot 5 + 3\cdot 3 \cdot (-1) \right]$

Finalmente sólo hay que resolver todas las operaciones y tendremos el determinante, vamos paso a paso, resolvamos todas las multiplicaciones:

$\Delta _{B} = 75 + 28 - 18 - [105 + 40 - 9]$

Ahora eliminemos los corchetes:

$\Delta_{B} = 75 + 28 - 18 - 105 - 40 + 9$

Finalmente procedamos a efectuar las sumas y restas:

$\Delta_{B} = -51$

¡Así que el determinante de nuestra matriz de $3\times 3$ es $-51$ !

¡Genial, ya sabes calcular determinantes de matrices $2 \times 2$ y matrices $3 \times 3$ !

Determinantes de sistemas de ecuaciones lineales

Hemos llegado a algo más peculiar, bastante sencillo y útil. El cálculo de determinantes de sistemas de ecuaciones lineales de $n\times n$ sirve para hallar los valores de las incógnitas, como bien podemos hallar los valores de las incógnitas de los sistemas de ecuaciones lineales de $2\times 2$ :

\begin{array}{l} x + 2y = 1 \\ x + y = 1 \end{array}

Donde:

$x = 1 \quad y = 0$

O en un sistema de ecuaciones $3\times 3$ :

\begin{array}{l} x + y + z = 1 \\x + 2y + z = 1 \\x + y + 3z = 1 \end{array}

Donde:

$x = 1 \quad y = 0 \quad z = 0$

El número de incógnitas dirá de qué tamaño es el sistema de ecuaciones lineales, si tiene dos incógnitas, el sistema de ecuaciones es de $2\times 2$ , si tiene tres incógnitas, el sistema de ecuaciones es de $3\times 3$ y así sucesivamente.

Para hallar los valores de las incógnitas se tiene que aplicar la regla de Cramer con la cual se divide los determinantes de las matrices de las incógnitas entre el determinante de la matriz del sistema. Veamos rápidamente el siguiente ejemplo:

\begin{array}{l} a_{11}x + a_{12}y + a_{13}z = r_{1} \\ a_{21}x + a_{22}y + a_{23}z = r_{2} \\ a_{31}x + a_{32}y + a_{33}z = r_{3} \end{array}

Nuestra matriz es la siguiente:

s =\left( \begin{array}{c c c | c} a_{11} & a_{12} & a_{13} & r_{1} \\ a_{21} & a_{22} & a_{23} & r_{2} \\ a_{31} & a_{32} & a_{33} & r_{3} \end{array}\right)

Para hallar los valores de las incógnitas, hallaremos el determinante de la matriz del sistema (recuerda que los valores de $r_{1}$ , $r_{2}$ y $r_{3}$ no se toman en cuenta para calcular la matriz del sistema del determinante de $s$ ):

\Delta_{s} = \left| \begin{array}{c c c} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right |

Haremos exactamente lo mismo que hicimos de la sumatoria del producto de las diagonales azules menos la sumatoria del producto de las diagonales rojas, lo mismo que hicimos más arriba del post:

\Delta_{s} = \begin{array}{|c c c | c c} a_{11} & a_{12} & a_{13} & a_{11} & a_{12} \\ a_{21} & a_{22} & a_{23} & a_{21} & a_{22} \\ a_{31} & a_{32} & a_{33} & a_{31} & a_{32} \end{array}

$\Delta_{s} = a_{11}\cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot a_{32} -$

$\left[ a_{31}\cdot a_{22} \cdot a_{13} + a_{32} \cdot a_{23} \cdot a_{11} + a_{33} \cdot a_{21} \cdot a_{12}\right]$

Hallaremos el determinante de $x$ , donde la matriz para el determinante de $x$ es la misma matriz del sistema sólo que en la primera columna vamos a escribir los valores de $r_{1}$ , $r_{2}$ y $r_{3}$ respectivamente:

x = \left[ \begin{array}{c c c} r_{1} & a_{12} & a_{13} \\ r_{2} & a_{22} & a_{23} \\ r_{3} & a_{32} & a_{33} \end{array}\right ]

Haremos exactamente lo mismo que hicimos de la sumatoria del producto de las diagonales azules menos la sumatoria del producto de las diagonales rojas:

\Delta_{x} = \begin{array}{|c c c | c c} r_{1} & a_{12} & a_{13} & r_{1} & a_{12} \\ r_{2} & a_{22} & a_{23} & r_{2} & a_{22} \\ r_{3} & a_{32} & a_{33} & r_{3} & a_{32} \end{array}

$\Delta_{x} = r_{1}\cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot r_{3} + a_{13} \cdot r_{2} \cdot a_{32} -$

$\left[ r_{3}\cdot a_{22} \cdot a_{13} + a_{32} \cdot a_{23} \cdot r_{1} + a_{33} \cdot r_{2} \cdot a_{12}\right]$

Para hallar el determinante para la matriz de $y$ , hacemos el mismo procedimiento como hicimos para la matriz de $x$ , tomamos la matriz del sistema pero ahora cambiaremos la segunda columna por los valores de $r_{1}$ , $r_{2}$ y $r_{3}$ respectivamente:

y = \left[ \begin{array}{c c c} a_{11} & r_{1} & a_{13} \\ a_{21} & r_{2} & a_{23} \\ a_{31} & r_{3} & a_{33} \end{array}\right ]

\Delta_{y} = \begin{array}{|c c c | c c} a_{11} & r_{1} & a_{13} & a_{11} & r_{1} \\ a_{21} & r_{2} & a_{23} & a_{21} & r_{2} \\ a_{31} & r_{3} & a_{33} & a_{31} & r_{3} \end{array}

$\Delta_{y} = a_{11}\cdot r_{2} \cdot a_{33} + r_{1} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot r_{3} -$

$\left[ a_{31}\cdot r_{2} \cdot a_{13} + r_{3} \cdot a_{23} \cdot a_{11} + a_{33} \cdot a_{21} \cdot r_{1}\right]$

Para hallar el determinante para la matriz de $z$ , hacemos el mismo procedimiento como hicimos para la matriz de $x$ , tomamos la matriz del sistema pero ahora cambiaremos la tercera columna por los valores de $r_{1}$ , $r_{2}$ y $r_{3}$ respectivamente:

z = \left[ \begin{array}{c c c} a_{11} & a_{12} & r_{1} \\ a_{21} & a_{22} & r_{2} \\ a_{31} & a_{32} & r_{3} \end{array}\right ]

\Delta_{z} = \begin{array}{|c c c | c c} a_{11} & a_{12} & r_{1} & a_{11} & a_{12} \\ a_{21} & a_{22} & r_{2} & a_{21} & a_{22} \\ a_{31} & a_{32} & r_{3} & a_{31} & a_{32} \end{array}

$\Delta_{z} = a_{11}\cdot a_{22} \cdot r_{3} + a_{12} \cdot r_{2} \cdot a_{31} + r_{1} \cdot a_{21} \cdot a_{32} -$

$\left[ a_{31}\cdot a_{22} \cdot r_{1} + a_{32} \cdot r_{2} \cdot a_{11} + r_{3} \cdot a_{21} \cdot a_{12}\right]$

Una vez que hallemos los determinantes de cada matriz, aplicaremos la regla de Cramer para obtener los valores finales:

$x = \cfrac{\Delta_{x}}{\Delta_{s}}$

$y = \cfrac{\Delta_{y}}{\Delta_{s}}$

$z = \cfrac{\Delta_{z}}{\Delta_{s}}$

Ejemplo de determinantes

En el siguiente ejemplo utilizaremos un sistema de ecuaciones $3\times 3$ con el cual utilizaremos el método de determinantes para hallar los valores de $x$ , $y$ y $z$ . Resolvamos el siguiente sistema de ecuaciones lineales:

\begin{array}{l} 4x - 2y + 2z = 36 \\ 2x + 4y - 5z = 28 \\ 6x - 3y + 2z = 24 \end{array}

Donde nuestra matriz se verá de la siguiente manera:

s = \left(\begin{array}{c c c | c} a_{11} & a_{12} & a_{13} & r_{1} \\ a_{21} & a_{22} & a_{23} & r_{2} \\ a_{31} & a_{32} & a_{33} & r_{3} \end{array}\right) = \left(\begin{array}{c c c | c} 4 & -2 & 2 & 36 \\ 2 & 4 & -5 & 28 \\ 6 & -3 & 2 & 24 \end{array}\right)

Para resolver el sistema de ecuaciones lineales mostrado, se tiene que hallar el determinante del sistema ( $s$ ), el determinante de $x$ , el determinante de $y$ y el determinante de $z$ , así que primero hallemos el determinante del sistema como lo hemos visto más arriba del post, agreguemos las dos columnas y efectuemos las operaciones correspondientes:

\Delta_{s} = \left | \begin{array}{c c c | c c} 4 & -2 & 2 & 4 & -2\\ 2 & 4 & -5 & 2 & 4\\ 6 & -3 & 2 & 6 & -3 \end{array}\right .

$\Delta_{s}=4 \cdot 4 \cdot 2 + (-2)\cdot(-5)\cdot 6 + 2 \cdot 2 \cdot(-3) -$

$\left[ 6\cdot4\cdot2 + (-3)\cdot(-5)\cdot 4 + 2\cdot2 \cdot(-2) \right]$

$\Delta_{s} = -20$

Ahora hallemos el $\Delta_{x}$ , cambiemos la primera columna por los valores de $r_{1}$ , $r_{2}$ y $r_{3}$

\Delta_{x} = \left | \begin{array}{c c c} 36 & -2 & 2 \\ 28 & 4 & -5 \\ 24 & -3 & 2 \end{array}\right |

Agreguemos las dos columnas más para que al momento de realizar la multiplicación se haga más fácil visualmente:

\Delta_{x} = \left | \begin{array}{c c c | c c} 36 & -2 & 2 & 36 & -2 \\ 28 & 4 & -5 & 28 & 4 \\ 24 & -3 & 2 & 24 & -3 \end{array}\right.

Ahora procedamos a escribir las operaciones correspondientes:

$\Delta_{x} = 36 \cdot 4 \cdot 2 + (-2)\cdot(-5)\cdot 24 + 2 \cdot 28 \cdot(-3) -$

$\left[ 24 \cdot 4 \cdot 2 + (-3)\cdot(-5)\cdot 36 + 2 \cdot 28 \cdot(-2) \right]$

Efectuando todas las operaciones tendremos el siguiente resultado:

$\Delta_{x} = -260$

Hallemos el $\Delta_{y}$ , cambiemos los valores de la segunda columna por los valores de $r_{1}$ , $r_{2}$ y $r_{3}$ :

\Delta_{y} = \left | \begin{array}{c c c} 4 & 36 & 2 \\ 2 & 28 & -5 \\ 6 & 24 & 2 \end{array}\right |

Procedamos a añadir las dos columnas más sólo para que se haga más fácil visualmente al realizar las operaciones:

\Delta_{y} = \left|\begin{array}{c c c | c c} 4 & 36 & 2 & 4 & 36 \\ 2 & 28 & -5 & 2 & 28\\ 6 & 24 & 2 & 6 & 24 \end{array} \right.

$\Delta_{y} = 4 \cdot 28 \cdot 2 + 36\cdot(-5)\cdot 6 + 2 \cdot 2 \cdot 24 -$

$\left[ 6 \cdot 28 \cdot 2 + 24 \cdot (-5) \cdot 4 + 2 \cdot 2 \cdot 36 \right]$

$\Delta_{y} = -760$

Finalmente hallemos el $\Delta_{z}$ , cambiemos los valores de la tercera columna por los valores de $r_{1}$ , $r_{2}$ y $r_{3}$ respectivamente:

\Delta_{z} = \left | \begin{array}{c c c} 4 & -2 & 36 \\ 2 & 4 & 28 \\ 6 & -3 & 24 \end{array}\right |

Ahora añadamos las dos columnas más para que se haga más fácil visualmente las operaciones:

\Delta_{z} = \left | \begin{array}{c c c | c c} 4 & -2 & 36 & 4 & -2 \\ 2 & 4 & 28 & 2 & 4 \\ 6 & -3 & 24 & 6 & -3 \end{array}\right .

$\Delta_{z} = 4 \cdot 4 \cdot 24 + (-2) \cdot 28 \cdot 6 + 36 \cdot 2 \cdot(-3) -$

$\left[ 6 \cdot 4 \cdot 36 + (-3) \cdot 28 \cdot 4 + 24 \cdot 2 \cdot(-2) \right]$

$\Delta_{z} = -600$

Con todos los determinantes hallados, podemos proceder a efectuar las divisiones que nos dirán cada valor de las incógnitas:

$x = \cfrac{\Delta_{x}}{\Delta_{s}} = \cfrac{-260}{-20} = 13$

$y = \cfrac{\Delta_{y}}{\Delta_{s}} = \cfrac{-760}{-20} = 38$

$z = \cfrac{\Delta_{z}}{\Delta_{s}} = \cfrac{-600}{-20} = 30$

¡Ahora sí! Nuestros resultados finales de nuestras incógnitas son:

$x = 13 \qquad y = 38 \qquad z = 30$

Gracias por estar en este momento con nosotros : )