Para começar com este post, primeiro mostraremos o resumo dos números reais com uma imagem simples e depois explicaremos cada componente da imagem.
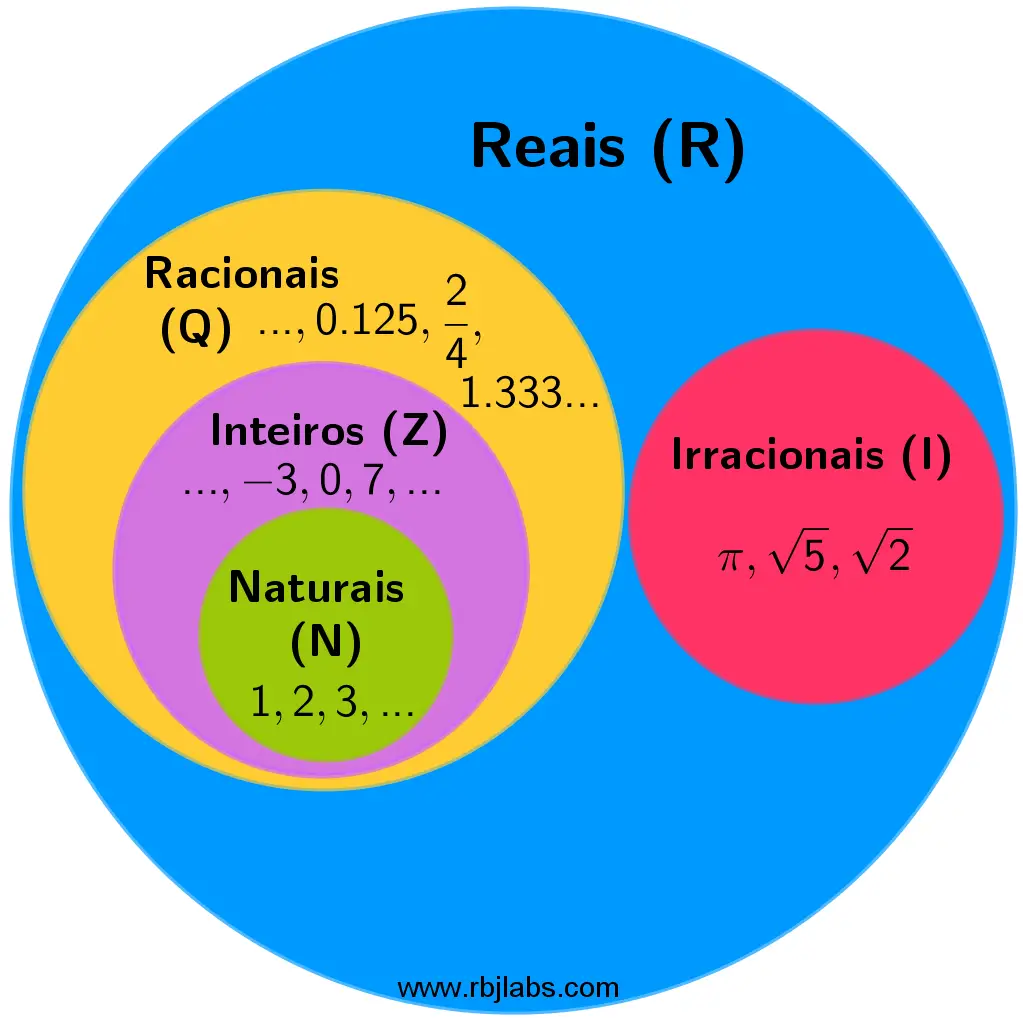
Números Reais (R)
Todos os números racionais e irracionais correspondem a um número real. Dos quais, os números racionais são compostos de números inteiros, números naturais, números negativos e zero.
Números reais são todos aqueles que podem ser representados dentro de uma reta numérica, não importa se o número é negativo, positivo, decimal racional ou irracional, inteiro ou zero.

Propriedades dos Números Reais
\begin{array}{c c} \hline \hline \begin{array}{c} \text{Propriedade} \\ \text{Comutativa} \end{array} & \begin{array}{c} a + b = b + a \qquad \qquad \quad a\times b = b \times a \\ \begin{array}{c} \text{O mesmo resultado é obtido independentemente da ordem }\\ \text{em que dois números são somados ou multiplicados.} \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Propriedade} \\ \text{Associativa} \end{array} & \begin{array}{c} \left(a + b \right) + c = a + \left(b + c \right) \qquad \left( a\times b\right)\times c = a\times \left( b \times c\right) \\ \begin{array}{c} \text{Se três números são somados ou multiplicados ao mesmo tempo} \\ \text{o mesmo resultado é obtido independentemente de qual} \\ \text{deles é adicionado ou multiplicado primeiro.} \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Propriedade} \\ \text{Distributiva} \end{array} & \begin{array}{c} a\times\left( b + c \right) = a \times b + a \times c \\ \left( b + c \right) \times a = b \times a + c \times a \\ \begin{array}{c} \text{Simplificação de expressões, forma a base} \\ \text{para métodos de fatoração.} \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Propriedade de } \\ \text{Identidade} \end{array} & \begin{array}{c} a + 0 = a \qquad a \times 1 = a \\ \begin{array}{c} \text{Se } a \text{ soma-se } 0 \text{, permanecerá } a \text{, e se é } \\ \text{multiplicado por } 1 \text{, também será o resultado } a. \end{array} \end{array} \\ \hline \hline \begin{array}{c} \text{Propriedade} \\ \text{Inversa} \end{array} & \begin{array}{c} a + (-a) = 0 \qquad a\times a^{-1} = 1 \\ \begin{array}{c} \text{Se } a \text{ é um número real, existe um único número } \\ \text{real denominado negativo} = -a \\ \text{Se } a \text{ não é zero, existe um único número} \\ \text{real denominado recíproco de } =a^{-1} \end{array} \end{array} \\ \hline \hline \end{array}Números Irracionais (I)
Números irracionais são todos aqueles números que não pode ser escrito por completo na forma decimal porque suas expressões decimais continuam indefinidamente sem apresentar nenhum padrão repetitivo. Podemos adicionar tantos decimais quanto pudermos a esses números, mas eles nunca terão um padrão de repetição em comparação com os números racionais.
Exemplos de números irracionais
Tenho certeza que você já viu o número \pi, deixe-me dizer que é um número irracional e da mesma forma existem muitos outros exemplos como os seguintes:
\sqrt{2} = 1.414213562...
\sqrt{3} = 1.732050808...
Números Racionais (Q)
Os números racionais são todos aqueles em que seus decimais terminam ou têm um padrão que se repete indefinidamente. Esses números racionais incluem as frações \left( \frac{x}{y} \right) onde o numerador (x) e o denominador (y) são inteiros e o denominador é diferente de zero.
Podemos realizar as operações básicas como somar, subtrair, multiplicar ou dividir entre dois números racionais e sempre obteremos outro número racional.
Exemplos de números racionais
Os números racionais podem ser qualquer fração contanto que o denominador seja diferente de zero:
\cfrac{1}{4} = 0.25
\cfrac{2}{3} = 0.666 \dots
O número \frac{2}{3} é um número racional simplesmente porque exibe um padrão de repetição para seus decimais.
Números Inteiros (Z)
Os inteiros são todos aqueles números naturais positivos, os negativos de cada número natural e zero. Podemos somar, subtrair e multiplicar e a divisão pode ser feita desde que o resultado não seja um número racional ou irracional.
Exemplos de números inteiros
Eles são simplesmente os números com os quais normalmente contamos mais os negativos de inteiros:
\dots , -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, \dots
Números Naturais (N)
Os números naturais são todos aqueles representados na reta numérica depois de zero. Podemos realizar todas as operações básicas, como adição, subtração, multiplicação e divisão, desde que o resultado seja outro número natural.
Exemplos de números naturais
Eles são simplesmente todos aqueles números inteiros positivos, não incluindo zero:
1, 2, 3, 4, 5, 6, 7, 8, \dots
4\times 3 = 12
5/5 = 1
Expoentes
Primeiro vamos definir o que é um expoente: Um expoente (n) é um número usado para indicar o número de vezes que um fator é multiplicado por si mesmo, assim como existem os subíndices, o expoente é um super-índice.
Exemplo de expoente
Se n é um número inteiro positivo, a^{n} significa que a será multiplicado por ele mesmo n vezes.
a^{n} = a \times a \times a \dots
2^{4} = 2 \times 2 \times 2 \times 2 = 16
11^{2} = 11 \times 11 = 121
Radicais
Vamos definir o que é um radical: um radical é uma expressão usada quando um número não pode ser simplificado eliminando alguma raiz n ou algum expoente fracionário. Portanto, podemos expressar um radical na forma de uma raiz para n ou expoente:
\sqrt[n]{a} = a^{\frac{1}{n}}
\sqrt[n]{b^{m}} = b^{\frac{m}{n}}
Exemplos de radicais
\sqrt[5]{4} = 4^{\frac{1}{5}}
\sqrt[6]{8^{3}} = 8^{\frac{3}{6}}
Operações com expoentes inteiros
Veremos 5 casos que são apresentados em operações com expoentes inteiros.
Caso 1
Quando dois expoentes de uma base comum são multiplicados, o resultado é igual à base (b) elevada à soma dos dois expoentes.
b^{n} \times b^{m} = b^{n + m}
Caso 2
Uma base a com um expoente m que é dividido pela mesma base a mas com um expoente n diferente, é igual à mesma base elevada pela subtração do expoente da base do numerador menos o expoente da base do denominador.
\cfrac{a^{m}}{a^{n}} = a^{m-n}
Caso 3
Um expoente n elevado a outro expoente m é igual à base elevada ao produto dos dois expoentes.
\left( a^{n}\right)^{m} = a^{n\times m}
Caso 4
O produto de dois números elevados a uma potência n é igual ao produto de cada número elevado a essa potência.
\left( a\times b\right)^{n} = a^{n} \times b^{n}
Caso 5
O quociente de dois números elevados a uma potência n é igual ao quociente de cada número elevado a essa potência.
\left( \cfrac{a}{b} \right)^{n} = \cfrac{a^{n}}{b^{n}}
Obrigado por estar connosco neste momento : )
