Vamos uma vez com a definição, depois veremos algumas características, depois citaremos teoremas com suas propriedades de logaritmos e finalmente dois exemplos de logaritmos.
Definição de logaritmo
O logaritmo de um número com uma determinada base é o expoente ao qual a base deve ser elevada para obter o número.
Vamos explicar essa definição um pouco mais. Temos que a relação que existe entre as funções exponencial e logarítmica é que os logaritmos são a função inversa das exponenciais, portanto, se tivermos uma função exponencial como:
y = b^{x}
O logaritmo dessa função, que também pode ser chamada como o inverso, é:
\log_{b}y = x
Mas como estamos acostumados a tratar x como os números e y como a função, escrevemos da seguinte maneira:
y = \log_{b}x
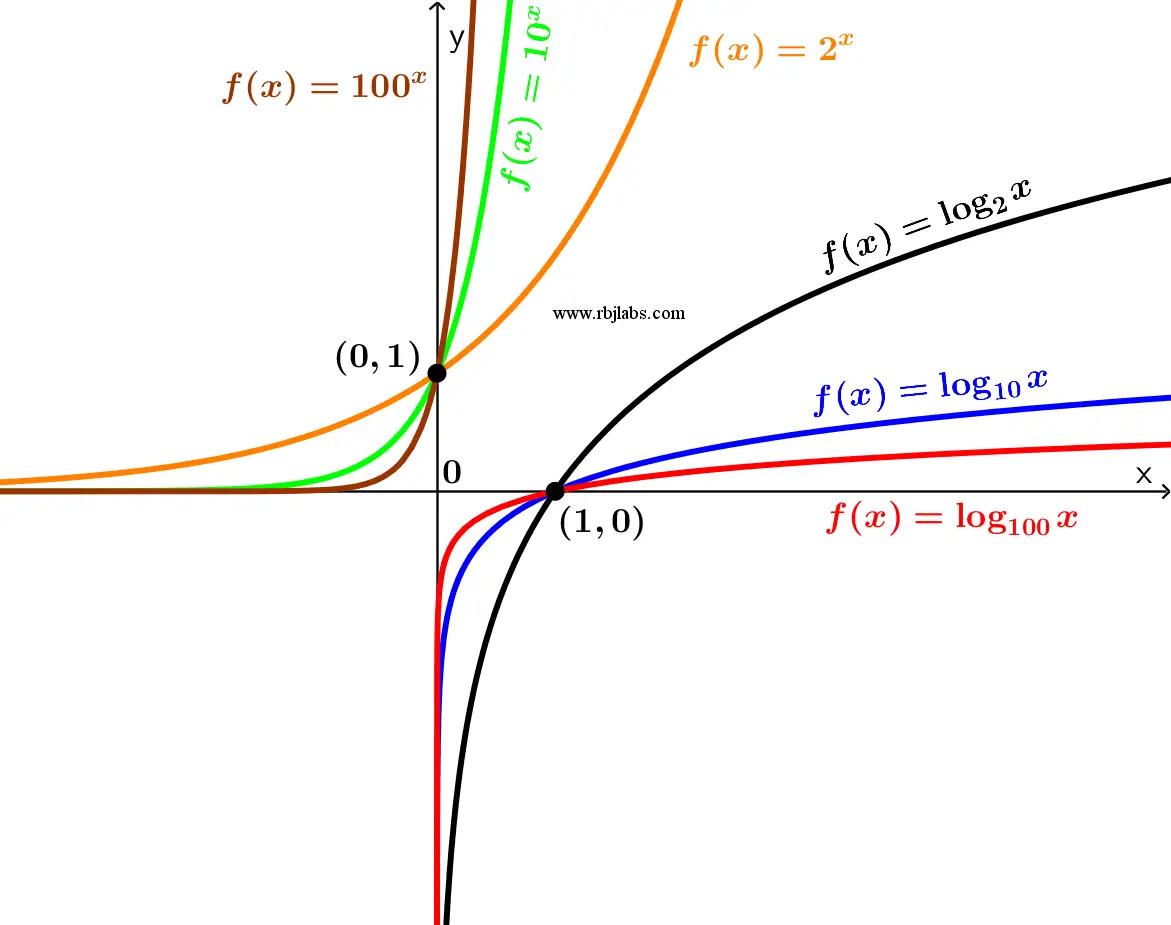
Como pode ser visto na Figura 1, as funções exponenciais com suas respectivas funções inversas ou logarítmicas podem ser apreciadas.
Continuando com a explicação, se tivermos a seguinte expressão:
\text{(1)} \quad \quad 6 = 2^{x}
Para encontrarmos o valor de x, precisamos entender que x está entre os valores de 2 e 3, pois 2^{2}=4 e 2^{3} = 8, agora começaremos a testar os valores para aproximarmos do nosso valor de 6. É por isso que temos logaritmos, já que os logaritmos também são expoentes. Tomando como representação o seguinte:
\text{(2)} \quad \quad \log_{2}6 = x
Da mesma forma, a única maneira de encontrar exatamente o valor de x é fazendo muitas iterações da expressão \text{(1)}, como explicamos, tentando valores entre 2 e 3 até temos um número com muitos decimais.
É por isso que o valor de x é representado como \log_{2}6 e não como um número com muitos decimais. Claro, se você pegar sua calculadora e colocar \log_{2}6, você receberá 2.5849..., que é um valor aproximado, mas muito próximo do resultado, já que a calculadora itera para dar sua resposta , apenas que a calculadora pode fazer muitas iterações em menos de um segundo.
A única maneira de ter o valor exato é fazer iterações infinitas, mas isso levaria um tempo infinito. É a graça da matemáticas.
Características dos logaritmos
Os logaritmos têm muitas peculiaridades como em muitas disciplinas de álgebra e agora vou mostrar essas características que os logaritmos têm para quando você vai fazer suas tarefas escolares.
- Apenas números positivos têm logaritmos reais. Números negativos não existem no campo de logaritmos, tais logaritmos são números complexos e, além disso, o logaritmo de zero é indefinido..
- Quando um número x aumenta, seu logaritmo b também aumenta. E quando x tende para o infinito, b também. Portanto, podemos escrever o seguinte:
\underset{x \to \infty} \lim \; \log_{b}x = \infty
- Para x < 1, \log_{b} x < 0; para x = 1, \log_{b} x = 0; e para x > 1, \log_{b} x > 0
- Quando x tende a zero, seu logaritmo tende a menos infinito, que é escrito da seguinte forma
\underset{ x \to 0} \lim \; \log_{b}x = - \infty
Propriedades dos logaritmos
Veremos as propriedades dos logaritmos nos seguintes teoremas, que são os resultados da transformação de quatro leis de expoentes:
- b^{x}\cdot b^{y} = b^{x+y}
- b^{x} \div b^{y} = b^{x-y}
- \left(b^{x} \right)^{n} = b^{nx}
- n\sqrt{b^{x}} = b^{x/n}
Dos quais escreveremos o seguinte
M = b^{x} \qquad \text{y} \qquad N=b^{y}
de onde:
x = \log_{b}M \qquad \text{y} \qquad y = \log_{b} N
Teorema 1
O logaritmo do produto ou da multiplicação de dois números positivos é igual à soma dos logaritmos de cada número.
\log_{b}MN = \log_{b}M + \log_{b}N
Se você tiver um número uma multiplicação, você pode separar com segurança essa multiplicação como uma soma de logaritmos.
Teorema 2
O logaritmo do quociente de dois números positivos é igual ao logaritmo do dividendo menos o logaritmo do divisor.
\log_{b}\cfrac{M}{N} = \log_{b}M - \log_{b}N
Como você pode ver, se o seu número é uma divisão, você pode converter essa expressão em uma subtração de logaritmo, basta lembrar que sempre será o logaritmo do numerador menos o logaritmo do denominador. Não escreva ao contrário porque isso é errado.
Teorema 3
O logaritmo da enésima potência de um número positivo é igual a n vezes o logaritmo do número.
\log_{b}M^{n} = n\log_{b}M
Esta é uma das vantagens que os logaritmos nos dão, que podemos ter o expoente como uma multiplicação de todo o logaritmo.
Teorema 4
O logaritmo da enésima raiz positiva real de um número positivo é igual ao resultado da divisão do logaritmo do número por n.
\log_{b}M^{n/a} = \cfrac{n}{a}\log_{b}M = \log_{b}\sqrt[a]{M^{n}}
Isso resulta em várias propriedades que os logaritmos nos oferecem:
\log_{b}b = 1
\log_{b}b^{n} = n
b^{\log_{b}N} = N
Teorema 5
O logaritmo de um número positivo N na base a, é igual ao logaritmo de N em outra base b, dividido pelo logaritmo de a na base b.
\log_{a}N = \frac{\log_{b}N}{\log_{b}a}
Exemplos trabalhados de logaritmos
Vejamos alguns exemplos com solução de logaritmos para que todos os conceitos são mais bem compreendidos
Exemplo 1 de logaritmos
Encontre o valor de x na seguinte expressão:
\log_{b}x = \log_{b}2 + 3 \log_{b}2 - \log_{b}4
Para começar com este exercício de logaritmos, faremos com que todos os logaritmos sejam multiplicados por 1, o que quero dizer é que podemos passar os 3 do termo 3\log_{b}2 como o expoente do 2:
\log_{b}x = \log_{b}2 + \log_{b}2^{3} - \log_{b}4
A próxima coisa é que vamos multiplicar os números da soma dos logaritmos, como diz nosso teorema 1 dos logaritmos:
\log_{b}x = \log_{b}2\cdot 2^{3} - \log_{b}4
Nesta etapa, podemos fazer dois coisas, ou multiplicar 2 por 2^{3} e então aplicar o teorema 2 dos logaritmos ou podemos primeiro aplicar o teorema 2 e depois multiplicar. Faremos o que dissemos primeiro:
\log_{b}x = \log_{b}16 - \log_{b}4
\log_{b}x = \log_{b}\frac{16}{4} = \log_{b} 4
E, finalmente, com base em uma de nossas propriedades do teorema 4 que diz:
b^{\log_{b}N} = N
Obtemos nosso resultado do valor de x:
b^{\log_{b}x}=x \ \ \text{y} \ \ b^{\log_{b}4} = 4
x = 4
Exemplo de logaritmos 2
Neste exemplo, usaremos logaritmos para encontrar a função inversa da seguinte função:
y = b^{x + 2}
Para começar com este exercício, o que faremos é aplicar a seguinte propriedade do nosso teorema 4:
\log_{b}b^{n} = n
Onde n é igual a x+2, então vamos aplicar um logaritmo a toda a expressão:
\log_{b}y = \log_{b}b^{x+2}
Usaremos o teorema 3 para passar o expoente de b multiplicando:
\log_{b}y = \left(x + 2 \right) \log_{b}b
Realizamos algumas operações simples:
\log_{b}y = x\log_{b}b + 2\log_{b}b
Agora o que faremos é passar nossa expressão 2\log_{b}b no outro lado da igualdade
\log_{b}y - 2\log_{b}b = x\log_{b}b
E estamos quase terminando, o que aplicaremos agora é uma de nossas propriedades do nosso teorema 4 que diz:
\log_{b}b=1
O que nos torna capazes de eliminar o logaritmo onde x é e onde 2 é:
\log_{b}y - 2 = x
Ordenando a igualdade, temos nosso resultado da função inversa encontrada:
x = \log_{b}y - 2
Obrigado por estar conosco neste momento : )
